方差、标准差、均方差、均方误差

方差是在概率论和统计学中衡量随机变量或一组数据时离散程度的度量。概率论中方差用来度量随机变量和其数学期望（即均值）之间的偏离程度。统计中的方差（样本方差）是每个样本值与全体样本值的平均数之差的平方值的平均数。方差可以用来描述变量的波动程度。

方差在统计学和概率分布中各有不同的定义，并有不同的公式。在统计学中，方差用来计算每一个变量（观察值）与总体均数之间的差异。为避免出现离均差总和为零，离均差平方和受样本含量的影响，统计学采用平均离均差平方和来描述变量的变异程度。总体方差计算公式：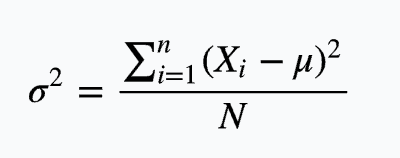

σ 的平方表示总体方差，X 表示变量，μ 表示总体的均值，N 表示总体样本数量。在实际项目中，总体均值难以得到时，应用样本统计量替代总体参数，经校正后，样本方差的计算公式：

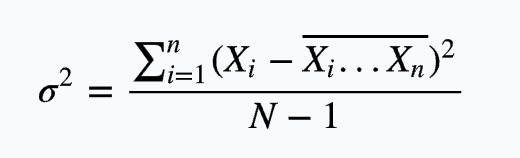
σ 的平方表示样本方差，X 表示变量，{X_i … X_n} 表示样本均值，N 表示样本数量。 之所以除以 N-1 而不是 N，是因为这样能使我们以较小的样本集更好地逼近总体的标准差，即统计上所谓的 「无偏估计」。由于方差是数据的平方，与检测值本身相差太大，难以直观的衡量，所以常用方差开根号换算回来，就成了标准差（Standard Deviation）用 σ 表示，公式如下：

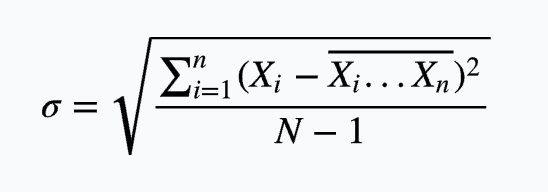
例如存在以下 python 代码:

import numpy as np 
data1 = [10, 30, 40, 50, 10]
data2 = [5, 20, 25, 80, 10]
print(np.mean(data1), np.var(data1), np.std(data1))
print(np.mean(data2), np.var(data2), np.std(data2))

输出结果：

28.0 256.0 16.0
28.0 726.0 26.94438717061496

可以看出两组数据的均值都是 28.0 但是方差以及标准差都是不一样，方差或标准差的值越大反应了数据波动就越大，反之则越稳定。

标准差在中文坏境中也被称为均方差，但不同于均方误差（mean squared error），均方误差是样本数据值偏离真实样本数据值的平方和的平均数，也即误差平方和的平均数，计算公式形式上接近方差，它的开方叫均方根误差，均方根误差才和标准差形式上接近。例如用 X 表示样本值，x 表示真实值，那么均方误差可用以下公式表示：

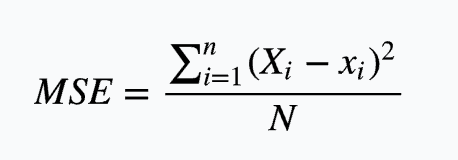
那么均分根误差可用以下公式表示：

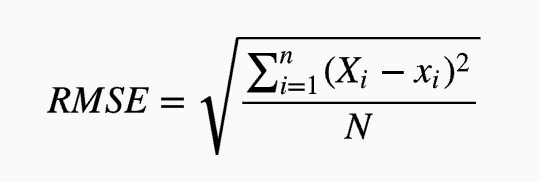
在机器学习中均方误差可以用来作为模型的损失函数，用来预测和回归，均方误差越小，说明模型预测的越准确，反之则越不准确。总的来说，均方差是数据样本与均值的关系，而均方误差是数据样本与真实值之间的关系，在实际工作中根据需要来选择使用均方差还是均方误差。